MATEMATIKA KELAS 9 MATERI BILANGAN BERPANGKAT DAN BENTUK AKAR

Sifat Sifat Bilangan Berpangkat

Berikut ini adalah beberapa sifat yang terdapat di dalam bilangan berpangkat, antara lian yakni:

1. Pangkat Bulat positif

Pengertian:

Sebagai contohnya a bilangan real serta n bilangan bulat positif. Notasi anakan menyatakan hasil kali dari bilangan a sebanyak n faktor. Sehingga dapat kita tuliskan menjadi:

an = a × a × a × … × a

Di mana : a x a x a x …. x a merupakan n faktor.

Keterangan:

• a merupakan basis bilangan berpangkat.
• n merupakan pangkat.

Sehingga, dapat kita ketahui bahwa:

1. Pada uraian di atas, maka kita sepakati, a1 cukup ditulis dengan a.
2. Tidak seluruh a0 dengan a bilangan real menyatakan 1. Pada saat a = 0 serta n = 0, maka an= 00, maka hasilnya tidak menentu.
3. Apabila n merupakan suatu variabel sebagai eksponen dari a, maka perlu kita perhatikan semesta variabel tersebut.
   Karena an = a × a × … × a sebanyak n faktor, ini hanya berlaku pada saat semesta n ∈N.

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

1. 24 = 2 x 2 x 2 x 2 =16
2. 32 = 3 x 3 = 9

2. Pangkat Bulat Negatif

Pengertian:

Untuk a bilangan real serta a ≠ 0, m bilangan bulat positif, maka di definisikan menjadi:

a-m = (1/a)m

Dari uraian di atas maka dapat dijelaskan lagi menjadi sebagai berikut:

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

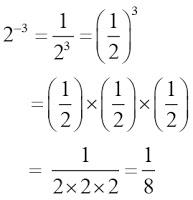
3. Pangkat Nol

Pengertian:

Untuk a bilangan real serta a ≠ 0, maka a0 = 1.

Kenapa a tidak boleh sama dengan nol?

Seperti yang sudah dijelaskan di atas, pada saat a = 0 maka a0 = 00, maka hasil­nya tidak menentu.

Sebagai contoh:

• 20 = 1
• 30 = 1

4. Sifat-sifat Pangkat Bulat Positif

Berikut adalah beberapa sifat dari bilangan pangkat bulat positif:

Sifat-1

Apabila a bilangan real, m serta n bilangan bulat positif maka

am × an = am+n

Pembuktian:

Si­fat di atas hanya berlaku apabila a merupakan bilangan real, m serta n merupakan bi­langan bulat positif. Apabila m dan n bukan bilangan bulat positif, maka sifat-1 tidak berlaku. Contohnya: a = 0 dan m = n = 0, tidak ber­laku.

Sebagai contoh:

22 x 23 = (2 x 2) x (2 x 2 x 2)

= 32

= 25

22 x 23 = 22+3

Sifat-2

Apabila a bilangan real serta a ≠ 0, m dan n bilangan bulat positif, sehingga:

Dalam sifat-2 tidak diperkenakan apabila a = 0, karena ben­tuk perpangkatan pada sifat-2 merupakan bentuk ra­sional.

Pada pecahan yang penyebutnya tidak lazim nol. Pada a = 0 dan m, n merupakan bilangan bulat positif, sehingga am atau an dimung­kinkan hasilnya 0.

Apabila hasil am serta an keduanya nol, maka hasil baginya tidak menentu.

Apabila am = 0 dan an ≠ 0, maka hasil baginya 0. Namun, apabila am ≠ 0 dan an = 0, maka hasil baginya tak ter­definisi.

Sebagi contoh:

25 / 23 = 2 x 2 x 2 x 2 x 2 / 2 x 2 x 2

= 4

= 22

= 25-3

Sifat-3

Jika a bilangan real serta a ≠ 0, m dan n merupakan bilangan bulat positif, maka (am)n = amn

Pembuktian:

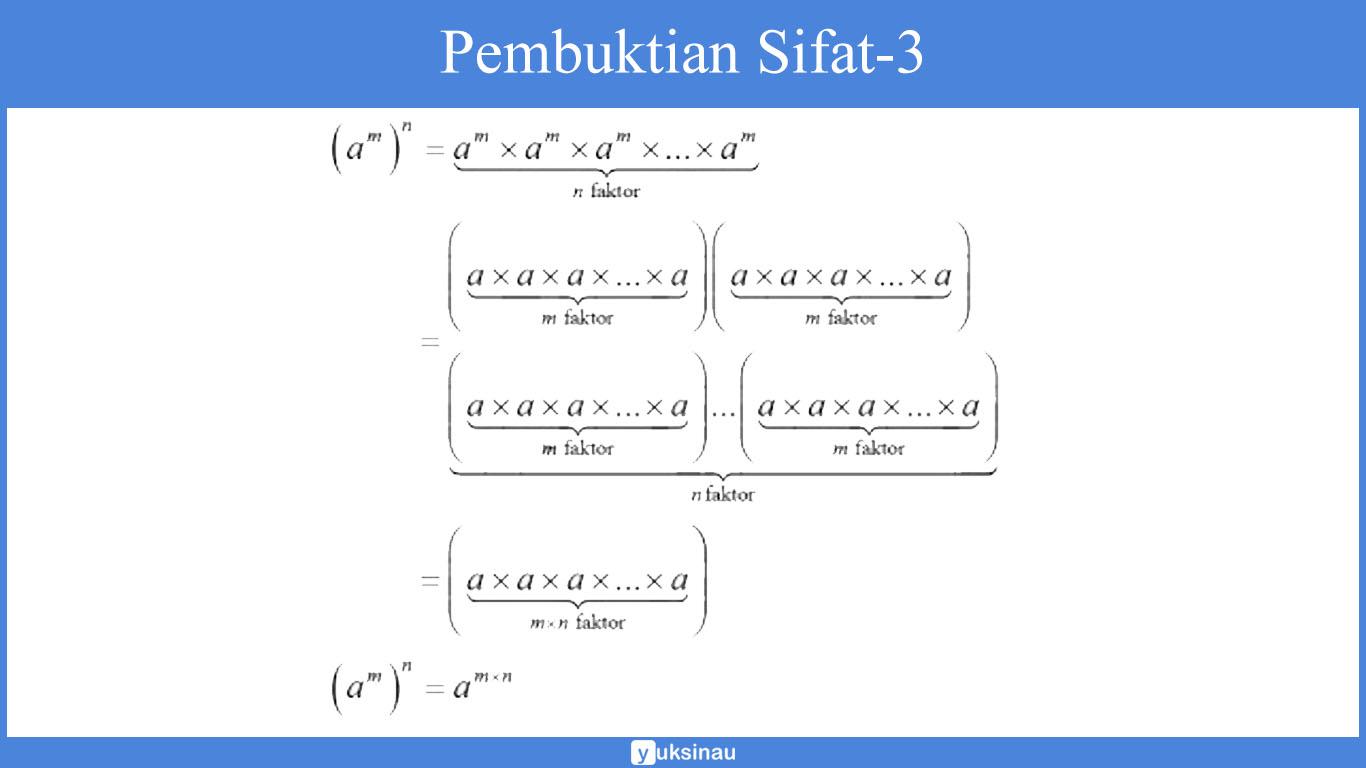
Sebagi contoh:
(23)2 = (23) x (23)

= (2 x 2 x 2) x (2 x 2 x 2)

= 2 x 2 x 2 x 2 x 2 x 2

= 26

Di mana (2 x 2 x 2) merupakan 3 faktor, 2 x 2 x 2 x 2 x 2 x 2 merupakan 6 faktor, dan lain sebagainya.

5. Pangkat Pecahan

Pengertian:

Contohnya a merupakan bilangan real dan a ≠ 0, serta m merupakan bilangan bulat positif, maka a1/m = p merupakan bilangan real positif, sehingga pm = a.

Sifat-sifat perpangkatan bilangan real dengan pangkat pecahan

Pengertian:

Contonya a merupakan bilangan real dan a ≠ 0, m, n merupakan bilangan bulat positif maka didefinisikan menjadi:

am/n = (a1/n)m

Misalkan a merupakan bilangan real dengan a > 0,

p/n dan m/n merupakan bilangan pecahan n ≠ 0, maka:

(am/n) = (ap/n) = (a)m+p/n

Pembuktian:

Apabila a merupakan bilangan real dengan a > 0, sehingga:

m/n dan p/q bilangan pecahan q, n ≠ 0, maka:

(am/n) = (ap/q) = (a)m/n+p/q

Rangkuman sifat bilangan berpangkat:

Untuk a, b merupakan bilangan bulat serta n, p, dan q merupakan bilangan bulat positif, maka berlaku:

Sifat Pangkat Rasional; 

anm=an−−−√m$$$$

Bilangan berpangkat rasional maksudnya adalah bilangan dengan pangkat berbentuk ab atau yang lebih dikenal dengan bentuk pecahan.

Pangkat rasional mempunyai nilai sama dengan bentuk akar.

Secara umum aturan perpangkatan bisa dilihat di bawah ini.

KERJAKAN SOAL DI BAWAH INI!