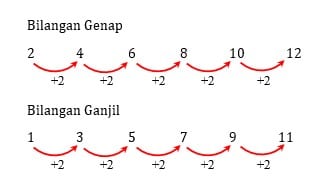
A. Pola Bilangan Ganjil
Pengertian pola bilangan ganjil adalah pola bilangan yang terbentuk dari bilangan-bilangan ganjil. Sedangkan pengertian bilangan ganjil adalah suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya.
Gambar Pola Bilangan Ganjil
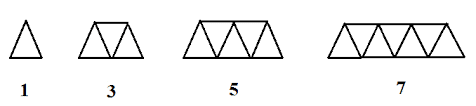
Rumus Pola Bilangan ganjil
1 , 3 , 5 , 7 , . . . , n , maka rumus pola bilangan ganjil ke n adalah:
Un = (2n)-1
Contoh Soal Pola Bilangan Ganjil
1 , 3 , 5 , 7 , . . . , ke 12. Berapakah pola bilangan ganjil ke 12 ?
Jawab :
U12 = (2.12)-1
U12 = 24 -1 = 23
B. Pola Bilangan Genap
Pengertian pola bilangan genap adalah pola bilangan yang terbentuk dari bilangan-bilangan genap . Bilangan genap adalah bilangan asli yang habis dibagi dua atau kelipatannya .
Pola bilangan genap adalah 2 , 4 , 6 , 8 , . . .
Gambar Pola Bilangan Genap
Rumus Pola Bilangan Genap
2 , 4 , 6 , 8 , . . . . , n maka rumus pola bilangan genap ke n adalah:
Un = 2n
Contoh Soal Pola Bilangan Genap
2 , 4 , 6 , 8 , . . . ke 12 . Berapakah pola bilangan genap ke 12 ?
Jawab :
Un = 2n
U12 = 2 x 12
U12 = 24
C. Pola Bilangan Persegi
Pengertian pola bilangan persegi adalah suatu barisan bilangan yang membentuk suatu pola persegi . Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 , . . .
Gambar Pola Bilangan Persegi
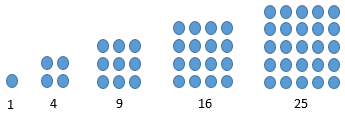
Rumus Pola Bilangan Persegi
1 , 4 , 9 , 16 , 25 , 36 , . . . , n maka rumus untuk mencari pola bilangan persegi ke-n adalah:
Un = n2
Contoh Pola Bilangan Persegi
Dari suatu barisan bilangan 1 , 4 , 9 , 16 , 25 , 36 , . . . ,ke 12 . Berapakah pola bilangan ke 12 dalam pola bilangan persegi ?
Jawab :
Un = n2
U12 = 122
U12 = 144
D. Pola Bilangan Persegi Panjang
Pengertian pola bilangan persegi panjang adalah suatu barisan bilangan yang membentuk pola persegi panjang . Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .
Gambar Pola Bilangan Persegi Panjang
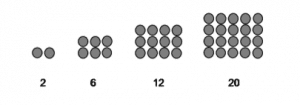
Rumus Pola Bilangan Persegi Panjang
2 , 6 , 12 , 20 , 30 , . . . n , maka rumus pola bilangan persegi panjang ke-n adalah:
Un = n . (n + 1)
Contoh Soal Pola Bilangan Persegi Panjang
Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , ke 12 . Berapakah pola bilangan persegi ke 12?
Jawab :
Un = n . (n+ 1)
U12 = 10 . (12 + 1)
U12 = 10 . 13
U12 = 130
E. Pola Bilangan Segitiga
Pengertian bola bilangan segitiga adalah suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga. Pola bilangan segitiga adalah 1 , 3 , 6 , 10 , 15 , . . .
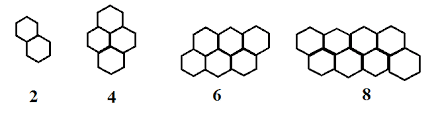
Gambar Pola Bilangan Segitiga
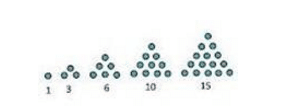
Rumus Pola Bilangan Segitiga
1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . Maka rumus pola bilangan segitiga ke n adalah:
Un = 1/2 n ( n + 1 )
Contoh Soal Pola Bilangan Segitiga
Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke 12 . Berapakah pola bilangan segitiga ke 12?
Jawab :
Un = 1/2 . n ( n + 1 )
U12 = 1/2 . 12 (12 + 1)
U12 = 6 (13)
U12 = 78
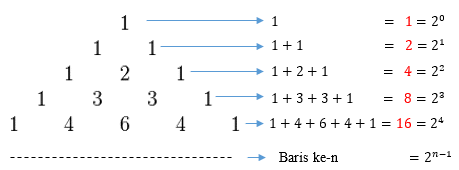
F. Pola Bilangan Fibonacci
Pengertian pola bilangan fibonacci adalah suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depannya. Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, ……
Perlu diketahui, 2 diperoleh dari hasil 1 + 1, 3 diperoleh dari hasil 2 + 1, 5 diperoleh dari hasil 3 + 2 dan seterusnya.
Rumus mencari suku ke-n pola bilangan fibonacci adalah Un =Un-1 + Un-2
Gambar Pola Bilangan Fibonacci
G. Pola Bilangan Segitiga Pascal
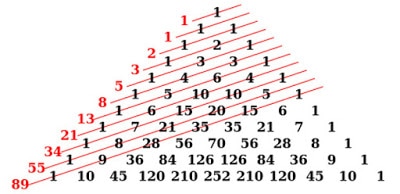
Bilangan pascal ditemukan oleh oleh orang Prancis bernama Blaise Pascal, sehingga dinamakan bilangan pascal. Bilangan pascal adalah bilangan yang terbentuk dari sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga.
Di dalam segitiga pascal, bilangan yang terdapat pada satu baris yang sama dijumlahkan menghasilkan bilangan yang ada di baris bawahnya. Jadi, pengertian pola bilangan pascal adalah suatu pola yang tersusun dari beberapa angka berdasarkan rumus: (perhatikan gambar pola bilangan pascal)
Pola bilangan pascal adalah 1, 2, 4, 8, 16, 24, 32, 64,…..
Rumus pola bilangan pascal :
2n-1
Contoh soal pola bilangan pascal:
tentukan suku ke 12 pola bilangan pascal:
jawab:
Un = 2n-1
U12 = 212-1
U12 = 211
U12 = 2048
H. Pola Bilangan Aritmatika
Pengertian pola bilangan aritmatika adalah pola bilangan dimana bilangan sebelum dan sesudahnya memiliki selisih yang sama. Contoh pola bilangan aritmatika adalah 2, 5, 8, 11, 14, 17, ….
Suku pertama dalam bilangan aritmatika disebut dengan awal ( a ) atau U1, sedangkan suku kedua adalah U2 dan seterusnya.
Selisih dalam barisan aritmatika disebut dengan beda dan dilambangkan dengan b.
Karena bilangan sebelum dan sesudahnya memiliki selisih yang sama, maka b = U2 – U1 = U3 – U2 = U4 – U3 = U5 – U4 = U6 – U5
Rumus mencari suku ke-n adalah Un = a + (n -1) b
Rumus mencari jumlah n suku pertama adalah Sn = n/2 (a + Un) atau Sn = n/2 (2 a + ( n-1 ) b )
Contoh Pola Bilangan Aritmatika
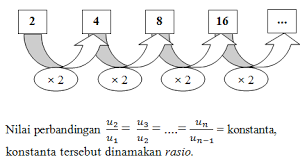
I. Pola Bilangan Geometri
Pengertian pola bilangan geometri adalah suatu bilangan hasil perkalian bilangan sebelumnya dengan suatu bilangan yang tetap.
Rumus suku ke-n adalah Un = arn-1
Contoh Pola Bilangan Geometri



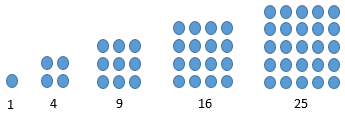





Komentar
Posting Komentar